Residence Time Distribution Analysis

Note

This notebook is located in the ./examples directory of the gwtransport repository.

Residence Time Distribution Analysis#

Learning Objectives#

  • Calculate residence time distributions from aquifer pore volume distributions

  • Understand the difference between infiltration to extraction and extraction to infiltration residence time perspectives

  • Analyze temporal variations in groundwater residence times

  • Apply residence time concepts to contaminant transport and water quality assessment

Overview#

This notebook demonstrates how to calculate residence time distributions from aquifer pore volume distributions and flow rates. Residence time quantifies how long water spends in the aquifer, which is crucial for understanding contaminant transport, groundwater vulnerability, and treatment efficiency.

Applications#

  • Contaminant transport predictions

  • Groundwater vulnerability assessment

  • Treatment efficiency evaluation

  • Water quality forecasting

  • Well capture zone analysis

Two Perspectives#

  • Infiltration to Extraction: How long until infiltrating water is extracted?

  • Extraction to Infiltration: How long ago was extracted water infiltrated?

Key Assumptions#

  • Stationary pore volume distribution

  • Advection-dominated transport

  • Known aquifer heterogeneity (from Example 1)

  • Conservative tracer behavior

Theoretical Background#

Residence Time Fundamentals#

Residence time in groundwater systems represents the travel time of water through the aquifer:

\[t_{residence} = \frac{V_{pore}}{Q} \cdot R_f\]

Where:

  • \(V_{pore}\): Pore volume along flow path [m³]

  • \(Q\): Flow rate [m³/day]

  • \(R_f\): Retardation factor [-] (1.0 for water, >1.0 for reactive tracers)

Infiltration to Extraction vs. Extraction to Infiltration Analysis#

Infiltration to Extraction Residence Time: Starting from infiltration time, calculates when water will be extracted

  • Used for: Contaminant arrival time predictions

  • Question: “When will this contamination reach the well?”

Extraction to Infiltration Residence Time: Starting from extraction time, calculates when water was infiltrated

  • Used for: Source identification and age dating

  • Question: “How old is the water we’re extracting now?”

Temporal Variability#

Residence times vary over time due to:

  • Seasonal flow rate changes

  • Aquifer heterogeneity

  • Extraction rate variations

[1]:

import warnings
from pathlib import Path

import matplotlib.pyplot as plt
import numpy as np

from gwtransport import gamma as gamma_utils
from gwtransport.examples import generate_example_data
from gwtransport.residence_time import residence_time

# Set random seed for reproducibility
np.random.seed(42)
plt.style.use("seaborn-v0_8-whitegrid")

print("Libraries imported successfully")

Libraries imported successfully

1. Data Setup and Aquifer Parameters#

We use aquifer parameters typically obtained from Example 1 (temperature-based characterization) and generate flow data for residence time analysis.

[2]:

df, tedges = generate_example_data(
    date_start="2020-01-01",
    date_end="2025-05-31",
    flow_mean=120.0,  # Base flow rate [m³/day]
    flow_amplitude=40.0,  # Seasonal flow variation [m³/day]
    flow_noise=5.0,  # Random daily fluctuations [m³/day]
    temp_infiltration_method="soil_temperature",  # Use real soil temperature data
    aquifer_pore_volume_gamma_mean=8000.0,  # True mean pore volume [m³]
    aquifer_pore_volume_gamma_std=400.0,  # True standard deviation [m³]
    retardation_factor=2.0,  # Thermal retardation factor [-]
)

print("Dataset Summary:")
print(f"Period: {df.index[0].date()} to {df.index[-1].date()}")
print(f"Mean flow: {df['flow'].mean():.1f} m³/day")
print(f"Flow range: {df['flow'].min():.1f} - {df['flow'].max():.1f} m³/day")
print(f"Aquifer parameters: {df.attrs['aquifer_pore_volume_mean']:.0f} ± {df.attrs['aquifer_pore_volume_std']:.0f} m³")

print("Dataset Summary:")
print(f"Period: {df.index[0].date()} to {df.index[-1].date()}")
print(f"Mean flow: {df['flow'].mean():.1f} m³/day")
print(f"Mean infiltration temperature: {df['temp_infiltration'].mean():.1f} °C")
print(f"Mean extraction temperature: {df['temp_extraction'].mean():.1f} °C")
print(f"True mean pore volume: {df.attrs['aquifer_pore_volume_mean']:.1f} m³")
print(f"True std deviation: {df.attrs['aquifer_pore_volume_std']:.1f} m³")

Dataset Summary:
Period: 2020-01-01 to 2025-05-31
Mean flow: 105.2 m³/day
Flow range: 8.1 - 170.0 m³/day
Aquifer parameters: 8000 ± 400 m³
Dataset Summary:
Period: 2020-01-01 to 2025-05-31
Mean flow: 105.2 m³/day
Mean infiltration temperature: 11.8 °C
Mean extraction temperature: 12.0 °C
True mean pore volume: 8000.0 m³
True std deviation: 400.0 m³

[3]:

# Discretize pore volume distribution for residence time calculation
n_bins = 1000  # High resolution for accurate calculations
bins = gamma_utils.bins(
    mean=df.attrs["aquifer_pore_volume_mean"], std=df.attrs["aquifer_pore_volume_std"], n_bins=n_bins
)

print(f"Pore volume distribution discretized into {n_bins} bins")
print(f"Bin range: {bins['expected_value'].min():.0f} - {bins['expected_value'].max():.0f} m³")
print(f"Mean residence time (no retardation): {df.attrs['aquifer_pore_volume_mean'] / df['flow'].mean():.1f} days")
print(
    f"Mean residence time (with retardation): {df.attrs['aquifer_pore_volume_mean'] / df['flow'].mean() * df.attrs['retardation_factor']:.1f} days"
)

Pore volume distribution discretized into 1000 bins
Bin range: 6722 - 9417 m³
Mean residence time (no retardation): 76.0 days
Mean residence time (with retardation): 152.0 days

2. Infiltration to Extraction Residence Time Analysis#

Calculate how long infiltrating water takes to be extracted. We compute residence times for both water flow (conservative tracer) and thermal transport (with retardation).

[4]:

print("Computing infiltration to extraction residence times...")

# Water residence time (no retardation)
rt_infiltration_to_extraction_water = residence_time(
    flow=df.flow,
    flow_tedges=tedges,
    aquifer_pore_volume=bins["expected_value"],
    retardation_factor=1.0,  # Conservative tracer (water flow)
    direction="infiltration_to_extraction",
)

# Thermal residence time (with retardation)
rt_infiltration_to_extraction_thermal = residence_time(
    flow=df.flow,
    flow_tedges=tedges,
    aquifer_pore_volume=bins["expected_value"],
    retardation_factor=df.attrs["retardation_factor"],  # Heat transport (slower)
    direction="infiltration_to_extraction",
)

print(f"Infiltration to extraction residence time arrays shape: {rt_infiltration_to_extraction_water.shape}")
print(
    f"({rt_infiltration_to_extraction_water.shape[0]} flow paths x {rt_infiltration_to_extraction_water.shape[1]} time steps)"
)

Computing infiltration to extraction residence times...
Infiltration to extraction residence time arrays shape: (1000, 1978)
(1000 flow paths x 1978 time steps)

[5]:

# Statistical analysis of residence time distributions
quantiles = [1, 10, 90, 99]  # Percentiles for uncertainty bounds
quantile_headers = [f"rt_infiltration_to_extraction_water_{q}%" for q in quantiles]

with warnings.catch_warnings():
    warnings.filterwarnings(action="ignore", message="Mean of empty slice")
    warnings.filterwarnings(action="ignore", message="All-NaN slice encountered")

    # Calculate mean residence times
    df["rt_infiltration_to_extraction_water_mean"] = np.nanmean(rt_infiltration_to_extraction_water, axis=0)
    df["rt_infiltration_to_extraction_thermal_mean"] = np.nanmean(rt_infiltration_to_extraction_thermal, axis=0)

    # Calculate percentiles for uncertainty analysis
    df[quantile_headers] = np.nanpercentile(rt_infiltration_to_extraction_water, quantiles, axis=0).T

print("Infiltration to extraction residence time statistics calculated")
print(f"Mean water residence time: {df['rt_infiltration_to_extraction_water_mean'].mean():.1f} days")
print(f"Mean thermal residence time: {df['rt_infiltration_to_extraction_thermal_mean'].mean():.1f} days")
print(
    f"Retardation effect: {df['rt_infiltration_to_extraction_thermal_mean'].mean() / df['rt_infiltration_to_extraction_water_mean'].mean():.1f}x"
)
print(
    f"({rt_infiltration_to_extraction_water.shape[0]} flow paths x {rt_infiltration_to_extraction_water.shape[1]} time steps)"
)

Infiltration to extraction residence time statistics calculated
Mean water residence time: 77.9 days
Mean thermal residence time: 151.6 days
Retardation effect: 1.9x
(1000 flow paths x 1978 time steps)

3. Infiltration to Extraction Residence Time Visualization#

Visualize how residence times vary over time and compare water vs. thermal transport.

[6]:

fig, ax = plt.subplots(2, 1, figsize=(14, 10), sharex=True)

# Flow rate subplot
ax[0].plot(df.index, df.flow, label="Discharge rate", color="steelblue", linewidth=1.2)
ax[0].set_ylabel("Flow Rate [m³/day]")
ax[0].set_title("Infiltration to Extraction Residence Time Analysis", fontsize=14, fontweight="bold")
ax[0].legend(loc="upper right")
ax[0].grid(True, alpha=0.3)

# Residence time subplot
ax[1].plot(
    df.index,
    df.rt_infiltration_to_extraction_water_mean,
    label="Mean (water, R=1.0)",
    color="blue",
    linewidth=1.5,
)
ax[1].plot(
    df.index,
    df.rt_infiltration_to_extraction_thermal_mean,
    label=f"Mean (thermal, R={df.attrs['retardation_factor']:.1f})",
    color="red",
    linewidth=1.5,
)

# Add uncertainty bounds
for q in quantiles:
    alpha_val = 0.4 if q in {10, 90} else 0.3
    linestyle = "--" if q in {1, 99} else "-."
    ax[1].plot(
        df.index,
        df[f"rt_infiltration_to_extraction_water_{q}%"],
        label=f"{q}% quantile (water)",
        color="blue",
        alpha=alpha_val,
        linewidth=0.8,
        linestyle=linestyle,
    )

ax[1].set_ylabel("Residence Time [days]")
ax[1].set_xlabel("Date")
ax[1].legend(loc="upper right", ncol=2, fontsize=9)
ax[1].grid(True, alpha=0.3)

# Add explanatory text
ax[1].text(
    0.02,
    0.02,
    "Infiltration to extraction: How many days until infiltrating water is extracted?",
    ha="left",
    va="bottom",
    transform=ax[1].transAxes,
    fontsize=11,
    bbox={"boxstyle": "round,pad=0.3", "facecolor": "wheat", "alpha": 0.8},
)

plt.tight_layout()

# Save the infiltration to extraction residence time plot
out_path = Path("02_Infiltration_to_Extraction_residence_time.png")
plt.savefig(out_path, dpi=300, bbox_inches="tight")
plt.show()

print(f"Infiltration to extraction residence time plot saved to: {out_path}")
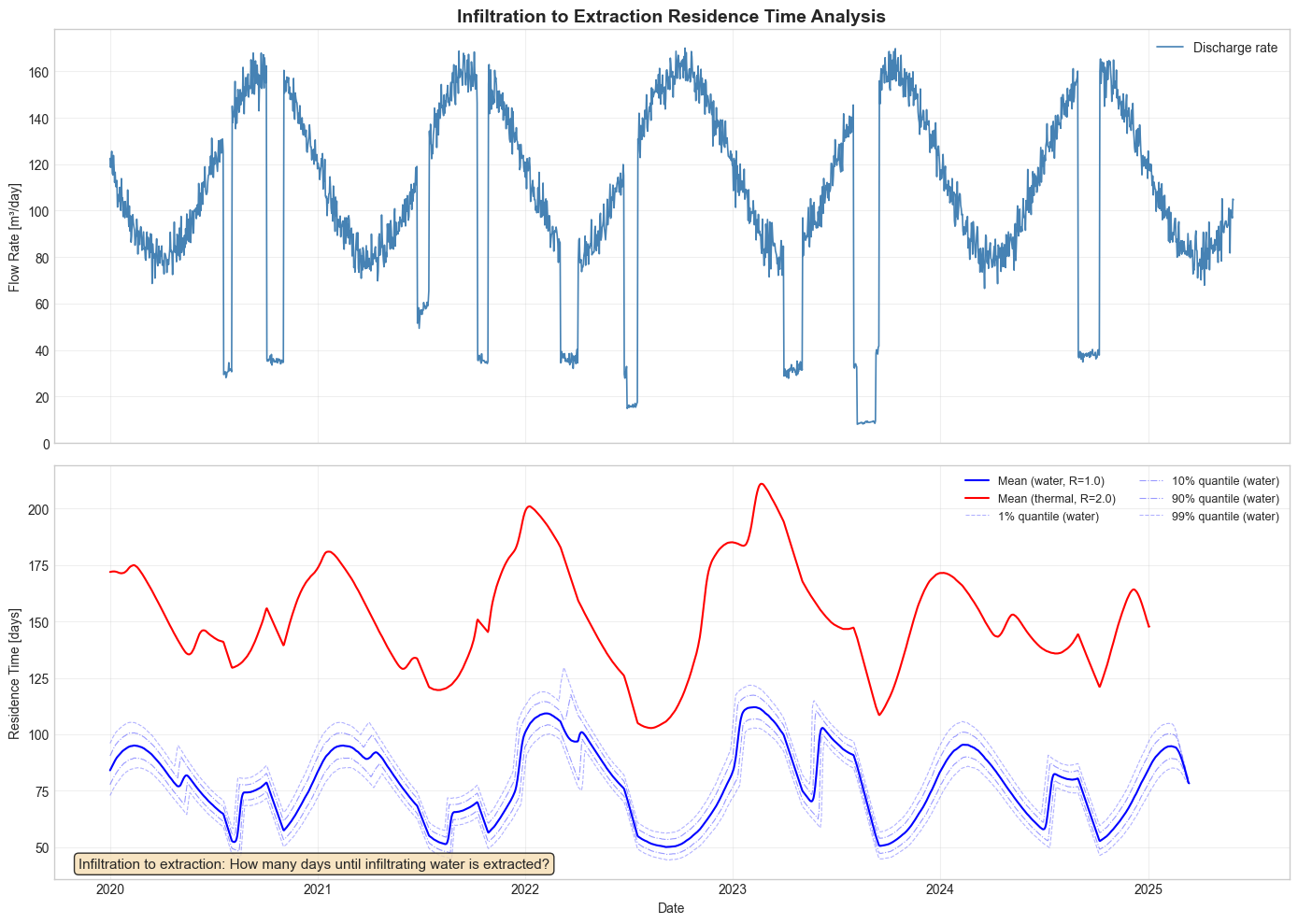
../_images/examples_02_Residence_Time_Analysis_11_0.png 
Infiltration to extraction residence time plot saved to: 02_Infiltration_to_Extraction_residence_time.png

4. Extraction to Infiltration Residence Time Analysis#

Calculate when currently extracted water was originally infiltrated. This perspective is crucial for source identification and age dating.

[7]:

print("Computing extraction to infiltration residence times...")

# Water residence time (no retardation)
rt_extraction_to_infiltration_water = residence_time(
    flow=df.flow,
    flow_tedges=tedges,
    aquifer_pore_volume=bins["expected_value"],
    retardation_factor=1.0,
    direction="extraction_to_infiltration",
)

# Thermal residence time (with retardation)
rt_extraction_to_infiltration_thermal = residence_time(
    flow=df.flow,
    flow_tedges=tedges,
    aquifer_pore_volume=bins["expected_value"],
    retardation_factor=df.attrs["retardation_factor"],
    direction="extraction_to_infiltration",
)

print(f"Extraction to infiltration residence time arrays shape: {rt_extraction_to_infiltration_water.shape}")

Computing extraction to infiltration residence times...
Extraction to infiltration residence time arrays shape: (1000, 1978)

[8]:

# Statistical analysis for extraction to infiltration residence times
quantile_headers_extraction_to_infiltration = [f"rt_extraction_to_infiltration_water_{q}%" for q in quantiles]

with warnings.catch_warnings():
    warnings.filterwarnings(action="ignore", message="Mean of empty slice")
    warnings.filterwarnings(action="ignore", message="All-NaN slice encountered")

    # Calculate mean residence times
    df["rt_extraction_to_infiltration_water_mean"] = np.nanmean(rt_extraction_to_infiltration_water, axis=0)
    df["rt_extraction_to_infiltration_thermal_mean"] = np.nanmean(rt_extraction_to_infiltration_thermal, axis=0)

    # Calculate percentiles
    df[quantile_headers_extraction_to_infiltration] = np.nanpercentile(
        rt_extraction_to_infiltration_water, quantiles, axis=0
    ).T

print("Extraction to infiltration residence time statistics calculated")
print(
    f"Mean extraction to infiltration water residence time: {df['rt_extraction_to_infiltration_water_mean'].mean():.1f} days"
)
print(
    f"Mean extraction to infiltration thermal residence time: {df['rt_extraction_to_infiltration_thermal_mean'].mean():.1f} days"
)

Extraction to infiltration residence time statistics calculated
Mean extraction to infiltration water residence time: 77.9 days
Mean extraction to infiltration thermal residence time: 151.6 days

5. Extraction to Infiltration Residence Time Visualization#

Show how the age of extracted water varies over time, revealing the temporal dynamics of groundwater flow.

[9]:

fig, ax = plt.subplots(2, 1, figsize=(14, 10), sharex=True)

# Flow rate subplot
ax[0].plot(df.index, df.flow, label="Discharge rate", color="steelblue", linewidth=1.2)
ax[0].set_ylabel("Flow Rate [m³/day]")
ax[0].set_title("Extraction to Infiltration Residence Time Analysis", fontsize=14, fontweight="bold")
ax[0].legend(loc="upper right")
ax[0].grid(True, alpha=0.3)

# Residence time subplot
ax[1].plot(
    df.index,
    df.rt_extraction_to_infiltration_water_mean,
    label="Mean (water, R=1.0)",
    color="green",
    linewidth=1.5,
)
ax[1].plot(
    df.index,
    df.rt_extraction_to_infiltration_thermal_mean,
    label=f"Mean (thermal, R={df.attrs['retardation_factor']:.1f})",
    color="orange",
    linewidth=1.5,
)

# Add uncertainty bounds for water
for q in quantiles:
    alpha_val = 0.4 if q in {10, 90} else 0.3
    linestyle = "--" if q in {1, 99} else "-."
    ax[1].plot(
        df.index,
        df[f"rt_extraction_to_infiltration_water_{q}%"],
        label=f"{q}% quantile (water)",
        color="green",
        alpha=alpha_val,
        linewidth=0.8,
        linestyle=linestyle,
    )

ax[1].set_ylabel("Residence Time [days]")
ax[1].set_xlabel("Date")
ax[1].legend(loc="upper right", ncol=2, fontsize=9)
ax[1].grid(True, alpha=0.3)

# Add explanatory text
ax[1].text(
    0.02,
    0.02,
    "Extraction to infiltration: How many days ago was the extracted water infiltrated?",
    ha="left",
    va="bottom",
    transform=ax[1].transAxes,
    fontsize=11,
    bbox={"boxstyle": "round,pad=0.3", "facecolor": "lightblue", "alpha": 0.8},
)

plt.tight_layout()

# Save the extraction to infiltration residence time plot
out_path = Path("02_Extraction_to_Infiltration_residence_time.png")
plt.savefig(out_path, dpi=300, bbox_inches="tight")
plt.show()

print(f"Extraction to infiltration residence time plot saved to: {out_path}")
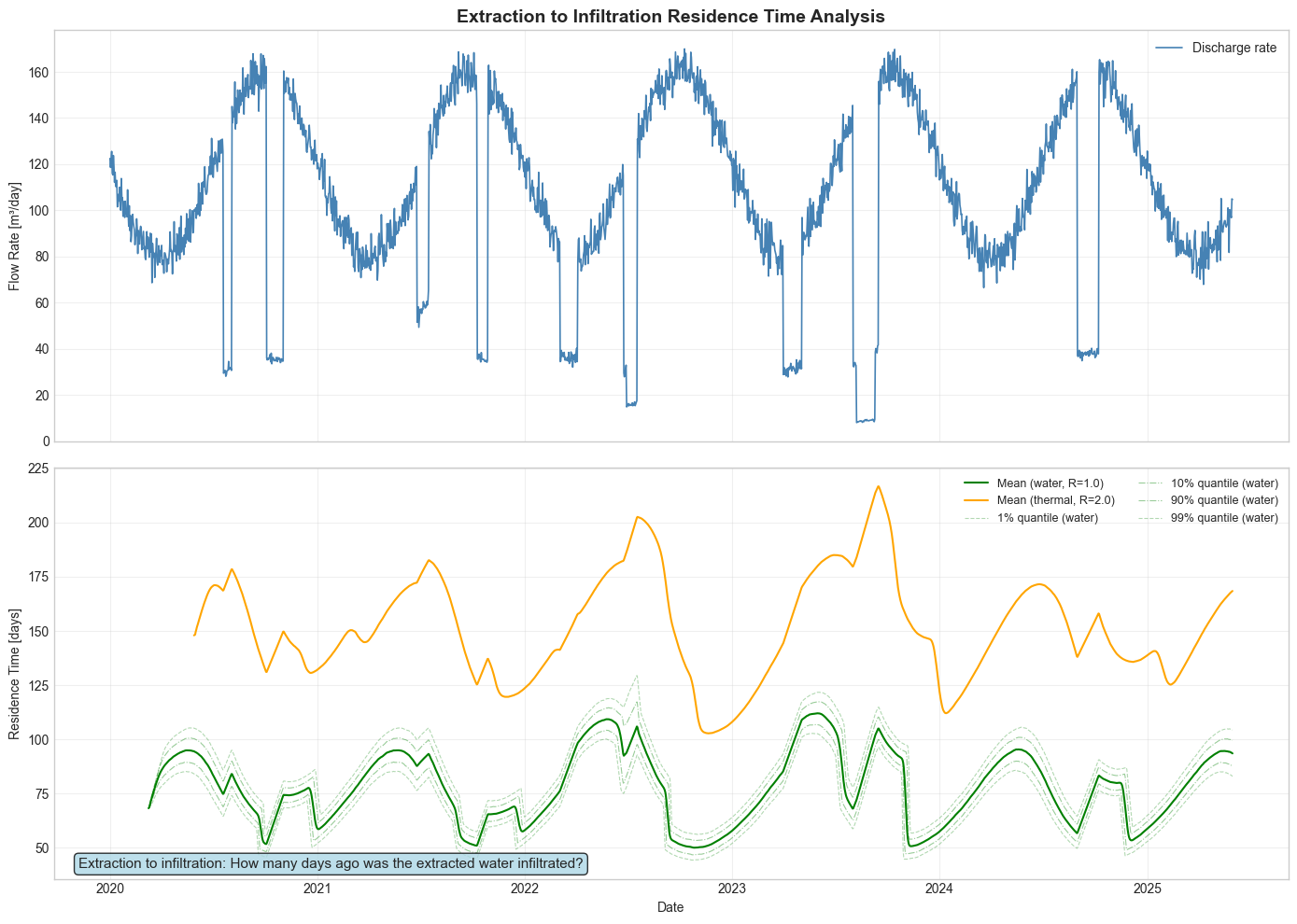
../_images/examples_02_Residence_Time_Analysis_16_0.png 
Extraction to infiltration residence time plot saved to: 02_Extraction_to_Infiltration_residence_time.png

Results & Discussion#

Flow Rate Dependencies#

Residence times show strong inverse correlation with flow rates:

  • High flows: Shorter residence times, faster transport

  • Low flows: Longer residence times, more retention

Infiltration to Extraction vs. Extraction to Infiltration Perspectives#

  • Similar mean values: Both perspectives yield comparable average residence times

  • Different temporal patterns: Timing of variability differs due to flow history effects

  • Practical applications: Choose perspective based on specific management question

Retardation Effects#

Thermal retardation factor of 2.0 effectively doubles residence times:

  • Important for temperature-based tracer studies

  • Affects timing of thermal breakthrough

  • Must be considered in heat transport applications

Engineering Applications#

Contaminant Transport:

  • Use infiltration to extraction analysis for spill response planning

  • Use extraction to infiltration analysis for source identification

Well Field Design:

  • Optimize pumping rates based on residence time requirements

  • Consider seasonal flow variations in planning

Water Quality Management:

  • Predict arrival times of contaminants

  • Assess natural attenuation potential

  • Design monitoring networks

Key Takeaways#

✅ Two Perspectives: Infiltration to extraction and extraction to infiltration residence times answer different but complementary questions

✅ Flow Rate Control: Higher flows lead to shorter residence times and faster transport

✅ Temporal Variability: Residence times vary seasonally due to flow rate changes

✅ Retardation Effects: Must account for tracer-specific retardation in transport analysis

✅ Uncertainty Quantification: Use percentile analysis to capture aquifer heterogeneity effects

✅ Practical Applications: Choose analysis perspective based on specific management objectives

Further Reading#

  • Previous Example: Aquifer Characterization using Temperature (Example 1)

  • Next Example: Pathogen Removal in Bank Filtration (Example 3)

  • Advanced Topics: Age dating methods, tritium analysis, residence time modeling

References#

  • McCallum, J.L., Cook, P.G., Brunner, P., & Burd, K. (2010). Solute transport along stream networks. Journal of Hydrology, 389(1-2), 214-226.

  • Goode, D.J. (1996). Direct simulation of groundwater age. Water Resources Research, 32(2), 289-296.

  • Varni, M., & Carrera, J. (1998). Simulation of groundwater age distributions. Water Resources Research, 34(12), 3271-3281.

Contents